栈与队列算法（3）——总结

date
tag , , ,

# 20. 有效的括号

20. 有效的括号

简单

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

  1. 左括号必须用相同类型的右括号闭合。
  2. 左括号必须以正确的顺序闭合。
  3. 每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = “()”

输出：true

示例 2：

输入：s = “()[]{}”

输出：true

示例 3：

输入：s = “(]”

输出：false

示例 4：

输入：s = “([])”

输出：true

示例 5：

输入：s = “([)]”

输出：false

提示：

  • 1 <= s.length <= 104
  • s 仅由括号 '()[]{}' 组成

# 栈

image-20251009115610957

用 map 来存括号的对应关系。

遍历到的左括号存入栈中，当遇到右括号时，与栈顶元素对应的右括号做匹配，若相等则说明括号有效，同时弹出栈顶元素，不等则括号无效。

另外需要注意，如果 len(s) 为奇数则一定不匹配，如果遇到右括号时栈中无元素，则说明多了右括号，不匹配返回false

如果匹配完毕，栈中无元素，说明所有括号都有效匹配。

func isValid(s string) bool {
    if len(s) % 2 != 0 {
        return false
    }
    // 用切片模拟栈
    stack := make([]rune, 0)

    // 哈希表 m 记录右括号对应的左括号
    m := make(map[rune]rune)
    m[')'] = '('
    m['}'] = '{'
    m[']'] = '['

    for _, v := range s {
        if v == '(' || v == '{' || v == '[' {
            stack = append(stack, v)
        } else {
            // 如果是右括号，先判断栈内是否有元素
            if len(stack) == 0 {
                return false
            }
            peek := stack[len(stack)-1]
            if peek != m[v] {
                return false
            } else {
                // 弹出栈顶元素
                stack = stack[:len(stack)-1]
            }
        }
    }
    // 如果栈中不包含元素，则代表完全匹配
    return len(stack) == 0
}

# 1047. 删除字符串中的所有相邻重复项

1047. 删除字符串中的所有相邻重复项

简单

给出由小写字母组成的字符串 s，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 s 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入："abbaca"
输出："ca"
解释：
例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

提示：

  1. 1 <= s.length <= 105
  2. s 仅由小写英文字母组成。
func removeDuplicates(s string) string {
    var stack []byte
    // 用字符串模拟栈，字符串尾部是栈入口，字符串头部是栈底部

    for i := 0; i < len(s); i++ {
        // 栈不空且与栈顶元素相等，弹出栈顶元素
        if len(stack) != 0 && s[i] == stack[len(stack)-1] {
            stack = stack[:len(stack)-1]
        } else {
            // 把元素放入栈
            stack = append(stack, s[i])
        }
    }
    return string(stack)
}

# 150. 逆波兰表达式求值

150. 逆波兰表达式求值

中等

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

  • 有效的算符为 '+'、'-'、'*' 和 '/' 。
  • 每个操作数（运算对象）都可以是一个整数或者另一个表达式。
  • 两个整数之间的除法总是 向零截断 。
  • 表达式中不含除零运算。
  • 输入是一个根据逆波兰表示法表示的算术表达式。
  • 答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

提示：

  • 1 <= tokens.length <= 104
  • tokens[i] 是一个算符（"+"、"-"、"*" 或 "/"），或是在范围 [-200, 200] 内的一个整数

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

  • 平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
  • 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

  • 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
  • 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中

# 栈

遍历 tokens 读到数字放入栈中，读到运算符就弹出栈顶的2个元素做运算，需要注意相减和相除时的元素顺序。

在判断元素是否是运算符，第一想到的是用哈希表。然而在用哈希表时遇到很多类型方面的问题。

首先是要判断元素是否在map中，最省空间的是用空struct，初始化时用 "+": {},，对map中元素赋值时用 set["+"] = struct{}{}

遍历的 token 是字符串，遇到例如 token“12” 时，不是单个字符 '1' 或 '2'，而是整体的 "12"字符串，长度为2。因此不能用 map[byte]struct{}，它只适合处理单字符场景。

把数字放入栈中，需要提前将 string 转为 int

下面的代码几乎没有用到库函数。

func evalRPN(tokens []string) int {
    stack := []int{}
    set := map[string]struct{} {
        "+": {},
        "-": {},
        "*": {},
        "/": {},
    }
    for i := 0; i < len(tokens); i++ {
        if _, ok := set[tokens[i]]; ok {
            // 从栈中取值做运算
            b := stack[len(stack)-1]
            a := stack[len(stack)-2]
            c := tokens[i]
            stack = stack[:len(stack)-2]
            switch {
                case c == "+":
                    stack = append(stack, a+b)
                case c == "-":
                    stack = append(stack, a-b)
                case c == "*":
                    stack = append(stack, a*b)
                case c == "/":
                    stack = append(stack, a/b) 
            }
        } else {
            // 把数字放入栈中
            num, _ := strconv.Atoi(tokens[i])
            stack = append(stack, num)
        }
    }
    return stack[len(stack)-1]
}

使用库函数，判断元素是否是数字

func evalRPN(tokens []string) int {
	stack := []int{}
	for _, token := range tokens {
		val, err := strconv.Atoi(token)
		if err == nil {
			stack = append(stack, val)
		} else {   // 如果err不为nil说明不是数字
			num1, num2 := stack[len(stack)-2], stack[(len(stack))-1]
			stack = stack[:len(stack)-2]
			switch token {
			case "+":
				stack = append(stack, num1+num2)
			case "-":
				stack = append(stack, num1-num2)
			case "*":
				stack = append(stack, num1*num2)
			case "/":
				stack = append(stack, num1/num2)
			}
		}
	}
	return stack[0]
}

# 239.滑动窗口最大值

239. 滑动窗口最大值

困难

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

示例 2：

输入：nums = [1], k = 1
输出：[1]

提示：

  • 1 <= nums.length <= 105
  • -104 <= nums[i] <= 104
  • 1 <= k <= nums.length

# 单调队列（仅适用于本题）

队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。

设计单调队列的时候，pop，和push操作要保持如下规则：

  1. pop(value)：如果窗口移除的元素value等于单调队列的出口元素，那么队列弹出元素，否则不用任何操作

    func (m *MyQueue) Pop(val int) {
    if !m.Empty() && val == m.Front() {
        m.queue = m.queue[1:]
    }
}

  2. push(value)：如果push的元素value大于入口元素的数值，那么就将队列入口的元素弹出，直到push元素的数值小于等于队列入口元素的数值为止

    func (m *MyQueue) Push(val int) {
    for !m.Empty() && val > m.Back() {
        m.queue = m.queue[:len(m.queue)-1]
    }
    m.queue = append(m.queue, val)
}

动画演示：

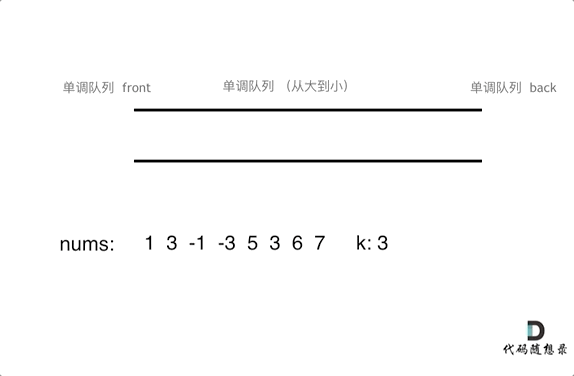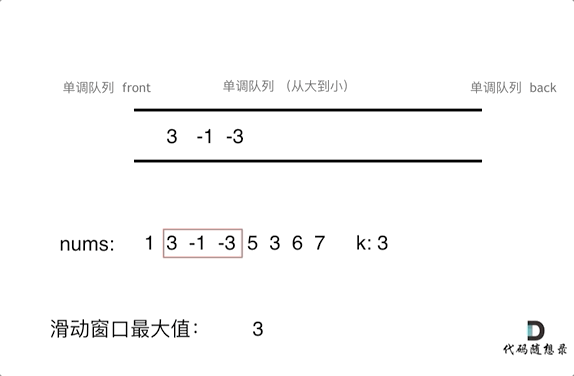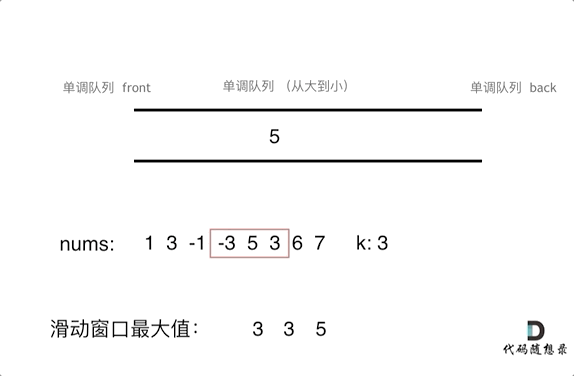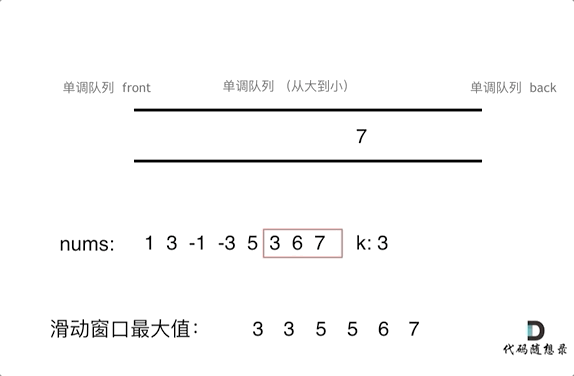
239.滑动窗口最大值-2

// 封装单调队列的方式解题
type MyQueue struct {
    queue []int
}

func NewMyQueue() *MyQueue {
    return &MyQueue{
        queue: make([]int, 0),
    }
}

func (m *MyQueue) Front() int {
    return m.queue[0]
}

func (m *MyQueue) Back() int {
    return m.queue[len(m.queue)-1]
}

func (m *MyQueue) Empty() bool {
    return len(m.queue) == 0
}

func (m *MyQueue) Push(val int) {
    for !m.Empty() && val > m.Back() {
        m.queue = m.queue[:len(m.queue)-1]
    }
    m.queue = append(m.queue, val)
}

func (m *MyQueue) Pop(val int) {
    if !m.Empty() && val == m.Front() {
        m.queue = m.queue[1:]
    }
}

func maxSlidingWindow(nums []int, k int) []int {
    queue := NewMyQueue()
    length := len(nums)
    res := make([]int, 0)
    // 先将前k个元素放入队列
    for i := 0; i < k; i++ {
        queue.Push(nums[i])
    }
    // 记录前k个元素的最大值
    res = append(res, queue.Front())

    for i := k; i < length; i++ {
        // 滑动窗口移除最前面的元素
        queue.Pop(nums[i-k])
        // 滑动窗口添加最后面的元素
        queue.Push(nums[i])
        // 记录最大值
        res = append(res, queue.Front())
    }
    return res
}

# 347. 前 K 个高频元素

347. 前 K 个高频元素

中等

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1：

输入：nums = [1,1,1,2,2,3], k = 2

输出：[1,2]

示例 2：

输入：nums = [1], k = 1

输出：[1]

示例 3：

输入：nums = [1,2,1,2,1,2,3,1,3,2], k = 2

输出：[1,2]

提示：

  • 1 <= nums.length <= 105
  • k 的取值范围是 [1, 数组中不相同的元素的个数]
  • 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的

进阶：你所设计算法的时间复杂度 必须 优于 O(n log n) ，其中 n 是数组大小。

# map+排序

先用 map 统计元素出现次数，再根据出现次数排序。

使用了 sort.Slice() 库函数

func topKFrequent(nums []int, k int) []int {
    ans := []int{}
    map_num := map[int]int{}
    // 统计元素出现次数
    for _, v := range nums {
        map_num[v]++
    }
    // 统计出现过的元素（去重）
    for k, _ := range map_num {
        ans = append(ans, k)
    }

    // 根据出现频率排序元素
    sort.Slice(ans, func(i, j int) bool {
        return map_num[ans[i]] > map_num[ans[j]]
    })
    return ans[:k]
}

# xmind 总结

🔗xmind 源文件

stack&queue

归档 友链
arrow_up
theme